0. 评价标准
- 时间复杂度
- 空间复杂度
- 稳定性(指的是,当两个元素的Key相等时,排序之前前面的元素,在排序之后仍然出现在前面)
| 排序方法 | 原理 | 最好时间 | 平均时间 | 最坏时间 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|---|
| 直接插入法 | 把元素逐一与已经排序的数据做比较,然后插入到合适位置 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 希尔排序 | O(n^1.333) | O(1) | 不稳定 | |||
| 直接选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 | |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 | |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 | |
| 快速排序 | O(nlogn) | O(nlogn) | O(n^2) | O(logn) | 不稳定 | |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 | |
| 基数排序(链式队列) | O(mn) | O(mn) | O(mn) | O(n) | 稳定 | |
| 基数排序(顺序队列) | O(mn) | O(mn) | O(mn) | O(mn) | 稳定 |
0.1 测试数据
我们把排序的对象抽象成 DataType 数据类型,之后会使用key作为排序的目标
class DataType:
def __init__(self, key, value):
self.key = key
self.value = value
def __repr__(self):
return 'key:{key},value:{value}'.format(key=self.key, value=self.value)
data = [DataType(64, 'data1'), DataType(5, 'data2'), DataType(7, 'data3'), DataType(89, 'data4'),
DataType(6, 'data5'),DataType(24, 'data6'), DataType(24, 'data7')]
1. 插入排序
1.1 直接插入排序
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
def InsertSort(data):
len_data = len(data)
for i in range(len_data - 1):
tmp = data[i + 1]
j = i
while (j > -1) and (tmp.key < data[j].key):
data[j + 1] = data[j]
j -= 1
data[j + 1] = tmp
return data
- 时间复杂度
- 最好复杂度。已经完成排序的序列,比较次数n-1,赋值次数2(n-1),复杂度$O(n)$
- 最坏复杂度。原序列是反序排列,复杂度是$O(n^2)$
- 平均复杂度。原序列随机排列,复杂度是$O(n^2/4)=O(n^2)$
- 空间复杂度$O(1)$
- 稳定性:稳定
1.2 希尔排序
为了减少数据移动操作。
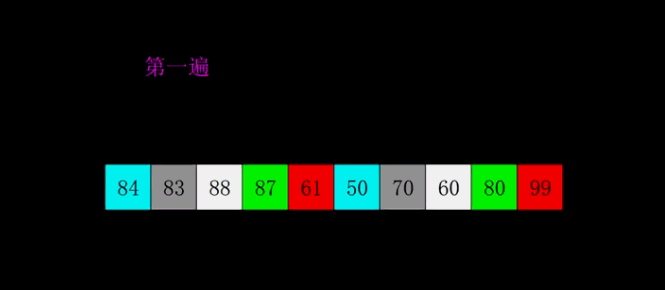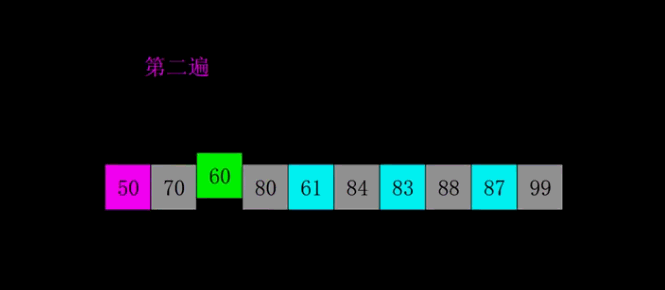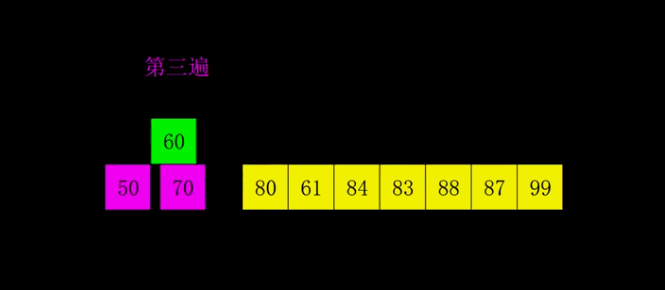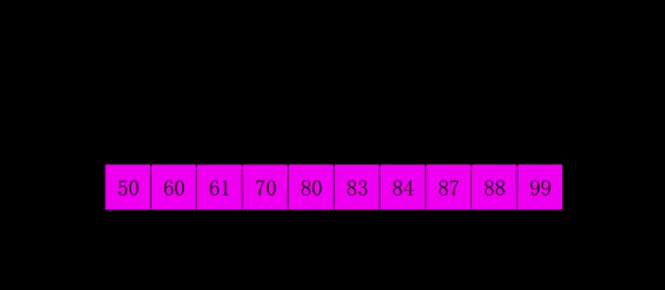
- 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列个数k,对序列进行k 趟排序;
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表4. 进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
2. 选择排序
2.1 直接选择排序
 思路:每次在池子中选择一个最小的,放到序列前面
思路:每次在池子中选择一个最小的,放到序列前面
- 初始状态:无序区为R[1..n],有序区为空;
- 第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- n-1趟结束,数组有序化了。
def SelectSort(data):
len_data = len(data)
for i in range(len_data - 1):
min_index = i
for j in range(i + 1, len_data): # 找到之后最小的
if data[j].key < data[min_index].key:
min_index = j
if min_index != i: # 如果最小的还是最开始的那个,不进行交换
data[min_index], data[i] = data[i], data[min_index]
return data
2.2 堆排序

# 懒省事,做个弊,代价就是不能针对第0章定义的 DataType 进行排序了
import heapq
def HeapSort(data):
heapq.heapify(data) # O(n)
res = []
while data:
res.append(heapq.heappop(data))
return res
HeapSort([[3, 9], [5, 2], [7, 9], [1, 3], [3, 5]])
3. 交换排序
3.1 冒泡排序
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
def BubbleSort(data):
len_data = len(data)
for i in range(1, len_data):
flag = 0 # 用于标记本次for循环是否曾经有交换动作。如果没有,说明已经排序完成,算法可以提前终止
for j in range(len_data - i):
if data[j].key > data[j + 1].key:
flag = 1
data[j], data[j + 1] = data[j + 1], data[j]
if flag == 0:
return data
return data
3.2 快速排序
下面这个图有些问题,不是快排。
快排思路
- 找一个基准值
- 使小于基准值的放到左边,大于基准值p的放到右边
- 对上面生成的每个子列,重复1,2
那么第二步如何实现呢?
- 两个指针指向两个端点,序号分别是i,j,后面的算法两个指针向中间移动
- 把基准值p拿出来,这样链上有个空位。例如,选左端点为p,这样i就是空位
- 右指针j向左移动,如果遇到比p小的,就填到空位i上。然后j就变成空位(看成空位,实际不必替换)。
- 如果i是空位,j向左移动;如果j是空位,i向右移动
- 直到i==j,然后把p填到i上
- 完成
4. 归并排序
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序(触发递归);
- 将两个排序好的子序列合并成一个最终的排序序列。
5. 基数排序

6. 大规模数据排序
2G内存,如何给20亿个int数据(8G)排序?
- 把8G数据分4片,每一片做排序
- 对于每片,每次读取1个值,比较后输出
- 这个题目有4片,n片的话第二步可以用堆排序
参考文献
朱战立:《数据结构-使用C语言》,西安交通大学出版社
https://www.cnblogs.com/onepixel/articles/7674659.html






